Java集合框架（二十）：TreeMap 源码解析

1、TreeMap 简介

TreeMap 使用红黑树存储元素，可以保证元素按key值的大小进行遍历。TreeMap底层是基于红黑树（Red-Black tree）实现，所以在学习TreeMap之前我们我们有必要先了解一下红黑树。

由于 TreeMap 底层采用一棵“红黑树”来保存集合中的 Entry，这意味 TreeMap 添加元素、取出元素的效率都比 HashMap 低：
🌂当向 TreeMap 添加元素时，需要通过循环找到新增 Entry 的插入位置。
🌂当从 TreeMap 中取出元素时，需要通过循环才能找到合适的 Entry。

但 TreeMap、TreeSet 相较于 HashMap、HashSet 的优势在于：
TreeMap 中的所有 Entry 总是按 key 根据指定排序规则保持有序状态，TreeSet 中所有元素总是根据指定排序规则保持有序状态。

1.1、红黑树（Red Black Tree）简述

红黑树是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。它是在1972年由鲁道夫·贝尔发明的，他称之为“对称二叉B树”，它现代的名字是在 Leo J. Guibas 和 Robert Sedgewick 于1978年写的一篇论文中获得的。它是复杂的，但它的操作有着良好的最坏情况运行时间，并且在实践中是高效的：它可以在O(log n)时间内做查找，插入和删除，这里的n是树中元素的数目。

红黑树中每个节点的值，都大于或等于在它的左子树中的所有节点的值，并且小于或等于在它的右子树中的所有节点的值，这确保红黑树运行时可以快速地在树中查找和定位的所需节点。

1.1.1、二叉查找树（BST）

为了更好的理解红黑树，必须先理解二叉查找树（BST）。其中红黑树又是一种特殊的排序二叉树。

二叉查找树（BST）是一种特殊结构的二叉树，可以非常方便地对树中所有节点进行排序和检索。

1.1.1.1、二叉查找树性质

二叉查找树（BST）要么是一棵空二叉树，要么是具有下列性质的二叉树：

🌂若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
🌂若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
🌂它的左、右子树也分别为排序二叉树。

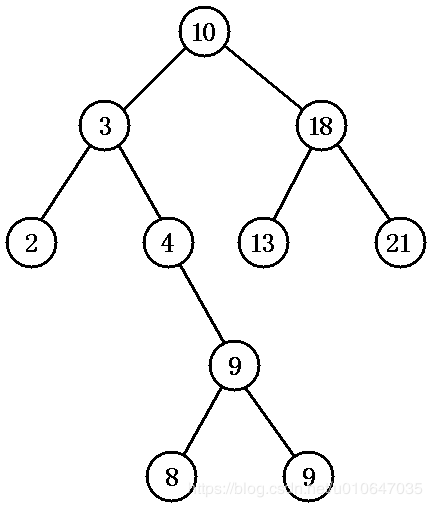
对排序二叉树，若按中序遍历就可以得到由小到大的有序序列：

1	{2，3，4，8，9，9，10，13，18，21}

创建排序二叉树的步骤，也就是不断地向排序二叉树添加节点的过程，向排序二叉树添加节点的步骤如下：

🌂以根节点当前节点开始搜索。
🌂新节点的值和当前节点的值比较。
🌂如果新节点的值更大，则以当前节点的右子节点作为新的当前节点；如果新节点的值更小，则以当前节点的左子节点作为新的当前节点。
🌂重复 2、3 两个步骤，直到搜索到合适的叶子节点为止。
🌂将新节点添加为第 4 步找到的叶子节点的子节点；如果新节点更大，则添加为右子节点；否则添加为左子节点。

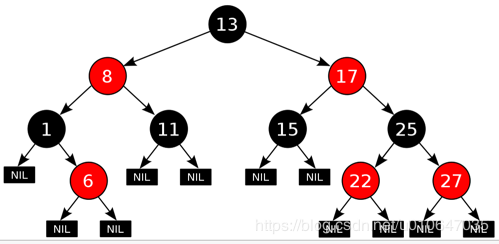
1.1.2、红黑树（Red Black Tree）

红黑树（Red Black Tree）是一种自平衡的二叉查找树。除了符合二叉查找树的的特性外，它还具有以下特性。

1.1.2.1、红黑树性质

🌂节点是红色或黑色。
🌂根节点是黑色。
🌂每个叶子节点都是黑色的空节点（NIL节点）。
🌂每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
🌂从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

2、TreeMap 源码分析

2.1、TreeMap 的定义

TreeMap 基于红黑树（Red-Black tree）实现。该映射根据其键的自然顺序进行排序，或者根据创建映射时提供的 Comparator 进行排序，具体取决于使用的构造方法。

TreeMap 的基本操作 containsKey、get、put 和 remove 的时间复杂度是 log(n) 。

TreeMap 是非同步的。它的iterator 方法返回的迭代器是fail-fast的。

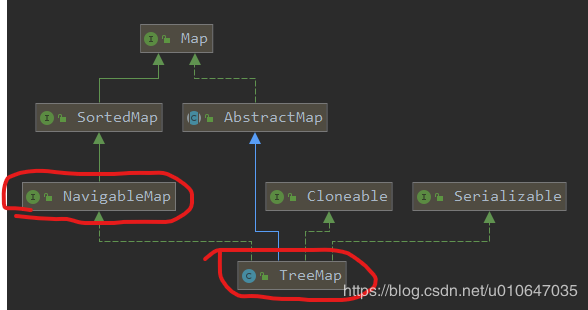
1
2
3

public class TreeMap<K,V>
    extends AbstractMap<K,V>
    implements NavigableMap<K,V>, Cloneable, java.io.Serializable

🌂TreeMap 继承于AbstractMap，所以它是一个Map，即一个key-value集合。
🌂TreeMap 实现了NavigableMap接口，意味着它支持一系列的导航方法。比如返回有序的key集合。
🌂TreeMap** 实现了Cloneable接口，意味着它能被克隆。
🌂TreeMap 实现了java.io.Serializable接口，意味着它支持序列化。
🌂NavigableMap 又接口继承**了 SortedMap 接口，SortedMap 接口规定了元素可以按key的大小来遍历，并且定义了一些返回部分map的方法

public interface SortedMap<K,V> extends Map<K,V> {
    // key的比较器
    Comparator<? super K> comparator();
    // 返回fromKey（包含）到toKey（不包含）之间的元素组成的子map
    SortedMap<K,V> subMap(K fromKey, K toKey);
    // 返回小于toKey（不包含）的子map
    SortedMap<K,V> headMap(K toKey);
    // 返回大于等于fromKey（包含）的子map
    SortedMap<K,V> tailMap(K fromKey);
    // 返回最小的key
    K firstKey();
    // 返回最大的key
    K lastKey();
    // 返回key集合
    Set<K> keySet();
    // 返回value集合
    Collection<V> values();
    // 返回节点集合
    Set<Map.Entry<K, V>> entrySet();
}

NavigableMap 是对 SortedMap 的增强，定义了一些返回离目标key最近的元素的方法。

public interface NavigableMap<K,V> extends SortedMap<K,V> {
    // 小于给定key的最大节点
    Map.Entry<K,V> lowerEntry(K key);
    // 小于给定key的最大key
    K lowerKey(K key);
    // 小于等于给定key的最大节点
    Map.Entry<K,V> floorEntry(K key);
    // 小于等于给定key的最大key
    K floorKey(K key);
    // 大于等于给定key的最小节点
    Map.Entry<K,V> ceilingEntry(K key);
    // 大于等于给定key的最小key
    K ceilingKey(K key);
    // 大于给定key的最小节点
    Map.Entry<K,V> higherEntry(K key);
    // 大于给定key的最小key
    K higherKey(K key);
    // 最小的节点
    Map.Entry<K,V> firstEntry();
    // 最大的节点
    Map.Entry<K,V> lastEntry();
    // 弹出最小的节点
    Map.Entry<K,V> pollFirstEntry();
    // 弹出最大的节点
    Map.Entry<K,V> pollLastEntry();
    // 返回倒序的map
    NavigableMap<K,V> descendingMap();
    // 返回有序的key集合
    NavigableSet<K> navigableKeySet();
    // 返回倒序的key集合
    NavigableSet<K> descendingKeySet();
    // 返回从fromKey到toKey的子map，是否包含起止元素可以自己决定
    NavigableMap<K,V> subMap(K fromKey, boolean fromInclusive,
                             K toKey,   boolean toInclusive);
    // 返回小于toKey的子map，是否包含toKey自己决定
    NavigableMap<K,V> headMap(K toKey, boolean inclusive);
    // 返回大于fromKey的子map，是否包含fromKey自己决定
    NavigableMap<K,V> tailMap(K fromKey, boolean inclusive);
    // 等价于subMap(fromKey, true, toKey, false)
    SortedMap<K,V> subMap(K fromKey, K toKey);
    // 等价于headMap(toKey, false)
    SortedMap<K,V> headMap(K toKey);
    // 等价于tailMap(fromKey, true)
    SortedMap<K,V> tailMap(K fromKey);
}

2.2、TreeMap 属性

/**
 * 比较器，如果没传则key要实现Comparable接口
 */
private final Comparator<? super K> comparator;

/**
 * 红黑树根节点
 */
private transient Entry<K,V> root;

/**
 * 元素个数
 */
private transient int size = 0;

/**
 * "fail-fast"集合修改次数
 */
private transient int modCount = 0;

TreeMap的本质是R-B Tree(红黑树)，它包含几个重要的成员变量： root, size, comparator。

🌂root 是红黑数的根节点。它是Entry类型，Entry是红黑数的节点，它包含了红黑数的6个基本组成成分：key(键)、value(值)、left(左孩子)、right(右孩子)、parent(父节点)、color(颜色)。Entry节点根据key进行排序，Entry节点包含的内容为value。
🌂红黑数排序时，根据Entry中的key进行排序；
🌂Entry 中的key比较大小是根据比较器comparator来进行判断的。
🌂size是红黑数中节点的个数。

Entry 类

// Red-black mechanics

    private static final boolean RED   = false;
    private static final boolean BLACK = true;

    /**
     * 红黑树中的节点
     */

    static final class Entry<K,V> implements Map.Entry<K,V> {
        K key;
        V value;
        // 左子节点
        Entry<K,V> left;
        // 右子节点
        Entry<K,V> right;
        // 父节点
        Entry<K,V> parent;
        // 当前节点颜色  
        boolean color = BLACK;

        /**
         * 用key，value和父节点构造一个Entry，默认为黑色
         */
        Entry(K key, V value, Entry<K,V> parent) {
            this.key = key;
            this.value = value;
            this.parent = parent;
        }

        /**
         * Returns the key.
         *
         * @return the key
         */
        public K getKey() {
            return key;
        }

        /**
         * Returns the value associated with the key.
         *
         * @return the value associated with the key
         */
        public V getValue() {
            return value;
        }

        /**
         * Replaces the value currently associated with the key with the given
         * value.
         *
         * @return the value associated with the key before this method was
         *         called
         */
        public V setValue(V value) {
            V oldValue = this.value;
            this.value = value;
            return oldValue;
        }

        public boolean equals(Object o) {
            if (!(o instanceof Map.Entry))
                return false;
            Map.Entry<?,?> e = (Map.Entry<?,?>)o;

            return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
        }

        public int hashCode() {
            int keyHash = (key==null ? 0 : key.hashCode());
            int valueHash = (value==null ? 0 : value.hashCode());
            return keyHash ^ valueHash;
        }

        public String toString() {
            return key + "=" + value;
        }
    }

Entry 类主要定义了树的节点和父节点引用，和红黑颜色属性，并对equals和hashCode进行重写，以利于比较是否相等。

2.3、TreeMap 构造函数

2.3.1、TreeMap()

/**
     * 默认构造函数，利用自然排序构造一个空的 TreeMap
     * 所有的key，必须实现Comparable接口
     * key 必须具备可比性，{@code k1.compareTo(k2)}不能抛出{@code ClassCastException}
     */
    public TreeMap() {
        comparator = null;
    }

2.3.2、TreeMap(Comparator<? super K> comparator)

/**
    * 根据指定的比较器构造一个空的 TreeMap
    */
   public TreeMap(Comparator<? super K> comparator) {
       this.comparator = comparator;
   }

2.3.3、TreeMap(Map<? extends K,? extends V> m)

/**
   * 根据给定的Map，构造一个包含与给定映射相同映射的新TreeMap，根据键的自然顺序排序。 插入新映射的所有键都必须实现Comparable接口。
   * 此外，所有的keykey必须具备可比性，k1.compareTo(k2) 不能抛出 ClassCastException 
   * 该方法的时间复杂度为n*log(n)
   */
  public TreeMap(Map<? extends K, ? extends V> m) {
      comparator = null;
      putAll(m);
  }

该构造方法调用putAll方法将Map中的所有元素加入到TreeMap中

/**
    * 将指定映射（map）中的所有映射复制到当前映射（TreeMap）。
    */
   public void putAll(Map<? extends K, ? extends V> map) {
       //获取map的大小
       int mapSize = map.size();
       // 如果TreeMap的大小是0,且map的大小不是0,且map是 SortedMap 类型的键值对    
       if (size==0 && mapSize!=0 && map instanceof SortedMap) {
           Comparator<?> c = ((SortedMap<?,?>)map).comparator();
           // 如果TreeMap和map的比较器相等，则将map的元素全部拷贝到TreeMap中
           if (c == comparator || (c != null && c.equals(comparator))) {
               ++modCount;
               try {
                   buildFromSorted(mapSize, map.entrySet().iterator(),
                                   null, null);
               } catch (java.io.IOException cannotHappen) {
               } catch (ClassNotFoundException cannotHappen) {
               }
               return;
           }
       }
       // 调用AbstractMap中的putAll(); AbstractMap中的putAll()又会调用 TreeMap的put() 
       super.putAll(map);
   }

如果Map里的元素是有序的，就调用 buildFromSorted 方法来拷贝Map中的元素，如果Map中的元素不是有序的，就调用**AbstractMap的putAll(map)**方法，该方法源码如下：

public void putAll(Map<? extends K, ? extends V> m) {
        for (Map.Entry<? extends K, ? extends V> e : m.entrySet())
            put(e.getKey(), e.getValue());
    }

AbstractMap的putAll(map)方法，是将Map中的元素一个个put（插入）到TreeMap中的，主要因为Map中的元素是无序的，因此要一个个插入到红黑树中，使其有序存放，并满足红黑树的性质。

2.3.4、TreeMap(SortedMap<K,? extends V> m)

/**
     * 根据给定是sortedMap，利用相同的排序方式构造一个新的treemap
     *
     */
    public TreeMap(SortedMap<K, ? extends V> m) {
        //获取sortedmap的comparator
        comparator = m.comparator();
        try {
            buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
        } catch (java.io.IOException cannotHappen) {
        } catch (ClassNotFoundException cannotHappen) {
        }
    }

首先获取给定的SortedMap的比较器，然后调用 buildFromSorted 方法，将 SortedMap 中的元素插入到TreeMap中。由于SortedMap中的元素是有序的，将SortedMap中的元素直接添加到TreeMap中即可。

2.4、put(K key, V value) 插入元素

TreeMap 添加元素实际上是向红黑树中添加节点，插入到指定位置后，再做调整，使其保持红黑树的特性。TreeMap 中使用 Entry 内部类代表节点，TreeMap 集合的 put(K key, V value) 方法实现了将 Entry 放入排序二叉树中，下面我们看一下源码的实现：

/**
     * 将指定的值与此映射中的指定键相关联。 如果映射先前包含键的映射，则替换旧值。
     *
     * @param key 与指定值关联的键
     * @param value 与指定键关联的值
     *
     * @return 与key关联的旧值，如果没有key的映射，则返回null。
     * @throws ClassCastException 如果指定的key无法与当前TreeMap中key进行比较
     */
    public V put(K key, V value) {
        // 根节点
        Entry<K,V> t = root;
        // 若红黑树为空，则直接创建一个根节点
        if (t == null) {
            compare(key, key); // type (and possibly null) check

            root = new Entry<>(key, value, null);
            size = 1;
            modCount++;
            return null;
        }
        // 记录比较结果
        int cmp;
        Entry<K,V> parent;
        // split comparator and comparable paths
        // 当前使用的比较器
        Comparator<? super K> cpr = comparator;
        // 如果比较器不为空，就是用指定的比较器来维护TreeMap的元素顺序
        if (cpr != null) {
        // do while循环，查找key要插入的位置
            do {
               // 记录上次循环的节点t
                parent = t;
                // 比较当前节点的key和新插入的key的大小
                cmp = cpr.compare(key, t.key);
                // 新插入的key小的话，则以当前节点的左子节点为新的比较节点
                if (cmp < 0)
                    t = t.left;
                // 新插入的key大的话，则以当前节点的右子节点为新的比较节点
                else if (cmp > 0)
                    t = t.right;
                // 如果当前节点的key和新插入的key相等，则覆盖原有的value
                else
                    return t.setValue(value);
            // 只有当t为null，没有要比较节点的时，代表已经找到新节点要插入的位置
            } while (t != null);
        }
        else {
            // 这里要求key不能为空，并且必须实现Comparable接口
            if (key == null)
                throw new NullPointerException();
            @SuppressWarnings("unchecked")
                Comparable<? super K> k = (Comparable<? super K>) key;
            // 查找新节点要插入的位置
            do {
                parent = t;
                cmp = k.compareTo(t.key);
                if (cmp < 0)
                    t = t.left;
                else if (cmp > 0)
                    t = t.right;
                else
                    return t.setValue(value);
            } while (t != null);
        }
        // 找到新节点的父节点后，创建节点对象
        Entry<K,V> e = new Entry<>(key, value, parent);
        // 如果新节点key的值小于父节点key的值，则插在父节点的左侧
        if (cmp < 0)
            parent.left = e;
        else
        // 如果新节点key的值大于等于父节点key的值，则插在父节点的右侧
            parent.right = e;
        // 插入新的节点后，为了保持红黑树平衡，对红黑树进行调整
        fixAfterInsertion(e);
        // map元素个数+1
        size++;
        modCount++;
        return null;
    }

每当添加新节点时，总是从树的根节点开始比较，将根节点当成当前节点：

🌂如果新增节点大于当前节点、并且当前节点的右子节点存在，则以右子节点作为当前节点；
🌂如果新增节点小于当前节点、并且当前节点的左子节点存在，则以左子节点作为当前节点；
🌂如果新增节点等于当前节点，则用新增节点覆盖当前节点，并结束循环
🌂重复以上几点，直到找到某个节点的左、右子节点不存在，将新节点添加该节点的子节点
🌂如果新节点比该节点大，则添加为右子节点；如果新节点比该节点小，则添加为左子节点。

2.4.1、插入修正操作

红黑树执行插入操作之后，要执行“插入修正操作”。
目的是：确保红黑树在插入节点之后，仍然是一颗红黑树，fixAfterInsertion 是新节点插入后对树进行调整的方法。

/** From CLR */
   private void fixAfterInsertion(Entry<K,V> x) {
       //新节点都为红色
       x.color = RED;
       //x存在且c不是根节点且x的父节点为红色
       while (x != null && x != root && x.parent.color == RED) {
           //如果x的父节点是祖父节点的左子树的话
           if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
               //取出祖父节点的右子树
               Entry<K,V> y = rightOf(parentOf(parentOf(x)));
               //如果祖父节点右子树是红色
               if (colorOf(y) == RED) {
                  //将父节点变成黑色
                   setColor(parentOf(x), BLACK);
                   //祖父节点的右子树变成黑色
                   setColor(y, BLACK);
                   //祖父节点变成红色
                   setColor(parentOf(parentOf(x)), RED);
                   //将x的引用指向祖父节点
                   x = parentOf(parentOf(x));
               } else {
               //如果祖父节点右子树是黑色
                   //如果x节点是父节点的右子树
                   if (x == rightOf(parentOf(x))) {
                       //x引用指向父节点
                       x = parentOf(x);
                       //左旋
                       rotateLeft(x);
                   }
                   //将x的父节点变成黑色
                   setColor(parentOf(x), BLACK);
                   //x的祖父节点变成红色
                   setColor(parentOf(parentOf(x)), RED);
                   //右旋
                   rotateRight(parentOf(parentOf(x)));
               }
           } else {
           //如果x的父节点是祖父节点的右子树
               //取出祖父节点的左子树
               Entry<K,V> y = leftOf(parentOf(parentOf(x)));
               //如果祖父节点左子树为红色
               if (colorOf(y) == RED) {
                   setColor(parentOf(x), BLACK);
                   setColor(y, BLACK);
                   setColor(parentOf(parentOf(x)), RED);
                   x = parentOf(parentOf(x));
               } else {
                //祖父节点左子树为黑色
                   //如果x是父节点的左子树
                   if (x == leftOf(parentOf(x))) {
                       //x引用指向父节点
                       x = parentOf(x);
                       //右旋
                       rotateRight(x);
                   }
                   //将x的父节点变成黑色
                   setColor(parentOf(x), BLACK);
                   //将x的祖父节点变成红色
                   setColor(parentOf(parentOf(x)), RED);
                   //左旋
                   rotateLeft(parentOf(parentOf(x)));
               }
           }
       }
       root.color = BLACK;
   }

2.5、remove(Object key) 删除元素

删除节点的时候调用的是deleteEntry(Entry<K,V> p)方法，这个方法主要是删除节点并且平衡红黑树

/**
     * 如果存在的话，根据指定的key从treemap中移除指定的键值对
     *
     * @param  key 要移除的键值对的key
     * @return 与key关联的旧值，如果没有key的映射，则返回null。
     */
    public V remove(Object key) {
        // 根据key查找到对应的节点对象
        Entry<K,V> p = getEntry(key);
        if (p == null)
            return null;
        // 取出 key 对应的value，返回使用
        V oldValue = p.value;
        // 删除节点
        deleteEntry(p);
        // 返回 key对应的value
        return oldValue;
    }

deleteEntry 方法只需按照二叉排序树的操作步骤实现即可，删除指定节点后，再对树进行调整。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

/**
     * 删除节点p，然后重新平衡树。
     */
    private void deleteEntry(Entry<K,V> p) {
        // 修改次数加一
        modCount++;
        // map 元素个数减一
        size--;

        // 如果被删除的节点p的左右子节点都不为空，则查找其替代节点（要删除的节点有两个子节点）
        if (p.left != null && p.right != null) {
            // 查找p的替代节点
            Entry<K,V> s = successor(p);
            p.key = s.key;
            p.value = s.value;
            // 将p指向替代节点
            p = s;
        } // p has 2 children
    
        // replacement 为替代节点p的继承者，p的左节点存在则用p的左节点替代，否则用p的右节点
        Entry<K,V> replacement = (p.left != null ? p.left : p.right);
        //要删除的节点只有一个子节点
        if (replacement != null) {
            // 将p的父节点赋给替代节点
            replacement.parent = p.parent;
            // 如果替代节点p的父节点为空，则p为根节点，将replacement设置为根节点
            if (p.parent == null)
                root = replacement;
            // 如果替代节点p是其父节点的左节点，则将replacement设置为其父节点的左节点
            else if (p == p.parent.left)
                p.parent.left  = replacement;
            else
            // 如果替代节点p是其父节点的右节点，则将replacement设置为其父节点的右节点
                p.parent.right = replacement;
    
            // Null out links so they are OK to use by fixAfterDeletion.
            // 将替代节点p的left、right、parent的指针都指向空，解除前后引用关系
            p.left = p.right = p.parent = null;
    
            // 如果替代节点p的颜色是黑色，则需要调整红黑树以保持其平衡
            if (p.color == BLACK)
                fixAfterDeletion(replacement);
        } else if (p.parent == null) { // return if we are the only node.
            // 如果要替代节点p没有父节点，代表p为根节点，直接删除即可
            root = null;
        } else { //  No children. Use self as phantom replacement and unlink.
            // 如果p的颜色是黑色，则调整红黑树
            if (p.color == BLACK)
                fixAfterDeletion(p);
            // 删除替代节点p
            if (p.parent != null) {
                if (p == p.parent.left)
                    p.parent.left = null;
                else if (p == p.parent.right)
                    p.parent.right = null;
                // 解除p对p父节点的引用
                p.parent = null;
            }
        }
    }

2.5.1、successor 获取后继节点

/**
    * 返回指定Entry的后继者，如果不存在，则返回null。
    */
   static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
       //t为null，则直接返回null
       if (t == null)
           return null;
       // 查找右子树的最左子树
       else if (t.right != null) {
           //获取右子树
           Entry<K,V> p = t.right;
           //循环遍历左子树，获取最后一个
           while (p.left != null)
               p = p.left;
           return p;
       } else {
       // 查找左子树的最右子树
           //获取父节点
           Entry<K,V> p = t.parent;
           //ch 指向 t
           Entry<K,V> ch = t;
           
           while (p != null && ch == p.right) {
               ch = p;
               p = p.parent;
           }
           return p;
       }
   }

当从二叉搜索树中删除一个节点之后，为了让它依然保持为二叉搜索树，程序必须对该二叉搜索树进行维护。维护可分为如下几种情况：

🌂被删除的节点是叶子节点，则只需将它从其父节点中删除即可。

🌂被删除节点 p 只有左子树，将 p 的左子树 pL 添加成 p 的父节点的左子树即可；被删除节点 p 只有右子树，将 p 的右子树 pR 添加成 p 的父节点的右子树即可。

🌂若被删除节点 p 的左、右子树均非空，有两种做法：

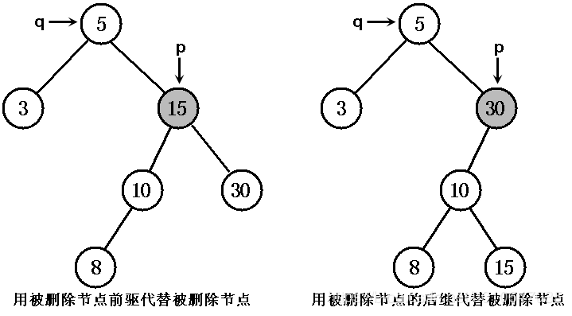
1.将 pL 设为 p 的父节点 q 的左或右子节点（取决于 p 是其父节点 q 的左、右子节点），将 pR 设为 p 节点的中序前趋节点 s 的右子节点（s 是 pL 最右下的节点，也就是 pL 子树中最大的节点）。

2.以 p 节点的中序前趋或后继替代 p 所指节点，然后再从原排序二叉树中删去中序前趋或后继节点即可。（也就是用大于 p 的最小节点或小于 p 的最大节点代替 p 节点即可）。

2.5.2、删除后修正操作

红黑树的删除遇到的主要问题就是被删除路径上的黑色节点减少，于是需要进行一系列旋转和着色

/** From CLR */
    private void fixAfterDeletion(Entry<K,V> x) {
        // while循环，保证要删除节点x不是根节点，并且是黑色（根节点和红色不需要调整）
        while (x != root && colorOf(x) == BLACK) {
            // 如果要删除节点x是其父节点的左子树
            if (x == leftOf(parentOf(x))) {
                // 取出要删除节点x的兄弟节点
                Entry<K,V> sib = rightOf(parentOf(x));
                
                // 如果删除节点x的兄弟节点是红色
                if (colorOf(sib) == RED) {
                    // 将x的兄弟节点颜色设置为黑色
                    setColor(sib, BLACK);
                    // 将x的父节点颜色设置为红色
                    setColor(parentOf (x), RED);
                    // 左旋x的父节点
                    rotateLeft( parentOf(x));
                    // 将sib重新指向旋转后x的兄弟节点 
                    sib = rightOf(parentOf (x));
                }

                // 如果x的兄弟节点的两个子节点都是黑色
                if (colorOf(leftOf(sib))  == BLACK &&
                    colorOf(rightOf (sib)) == BLACK) {
                    // 将兄弟节点的颜色设置为红色
                    setColor(sib, RED);
                    // 将x的父节点指向x
                    x = parentOf(x);
                } else {
                    // 如果x的兄弟节点右子节点是黑色，左子节点是红色
                    if (colorOf(rightOf(sib)) == BLACK) {
                        // 将x的兄弟节点的左子节点设置为黑色
                        setColor(leftOf (sib), BLACK);
                        // 将x的兄弟节点设置为红色
                        setColor(sib, RED);
                        // 右旋x的兄弟节点
                        rotateRight(sib);
                        // 将sib重新指向旋转后x的兄弟节点
                        sib = rightOf(parentOf (x));
                    }
                    // 如果x的兄弟节点右子节点是红色
                    setColor(sib, colorOf (parentOf(x)));
                    // 将x的父节点设置为黑色
                    setColor(parentOf (x), BLACK);
                    // 将x的兄弟节点的右子节点设置为黑色
                    setColor(rightOf (sib), BLACK);
                    // 左旋x的父节点
                    rotateLeft( parentOf(x));
                    // 达到平衡，将x指向root，退出循环
                    x = root;
                }
            } else { // symmetric
                // 如果要删除节点x是其父亲的右孩子，同上逻辑
                Entry<K,V> sib = leftOf(parentOf(x));

                if (colorOf(sib) == RED) {
                    setColor(sib, BLACK);
                    setColor(parentOf(x), RED);
                    rotateRight(parentOf(x));
                    sib = leftOf(parentOf(x));
                }

                if (colorOf(rightOf(sib)) == BLACK &&
                    colorOf(leftOf(sib)) == BLACK) {
                    setColor(sib, RED);
                    x = parentOf(x);
                } else {
                    if (colorOf(leftOf(sib)) == BLACK) {
                        setColor(rightOf(sib), BLACK);
                        setColor(sib, RED);
                        rotateLeft(sib);
                        sib = leftOf(parentOf(x));
                    }
                    setColor(sib, colorOf(parentOf(x)));
                    setColor(parentOf(x), BLACK);
                    setColor(leftOf(sib), BLACK);
                    rotateRight(parentOf(x));
                    x = root;
                }
            }
        }

        setColor(x, BLACK);
    }

2.6、get(Object key) 获取元素

相对于新增和删除元素来说，获取元素是如此的简单，按照二叉树的遍历查找即可。

/**
     * 返回指定键映射到的值，如果此映射不包含键的映射，则返回null。
     *
     * 返回值null不一定表示映射不包含键的映射; 集合中也可能将键明确映射为null。 containsKey操作可用于区分这两种情况。
     *
     */
    public V get(Object key) {
        Entry<K,V> p = getEntry(key);
        return (p==null ? null : p.value);
    }
    
     /**
     * 根据给定给定key，返回元素，如果不存在，则返回null
     *
     */
    final Entry<K,V> getEntry(Object key) {
        // Offload comparator-based version for sake of performance
        // 如果存在 comparator，调用 getEntryUsingComparator
        if (comparator != null)
            return getEntryUsingComparator(key);
        if (key == null)
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
            Comparable<? super K> k = (Comparable<? super K>) key;
        Entry<K,V> p = root;
        //利用二叉树性质，进行循环搜索
        while (p != null) {
            int cmp = k.compareTo(p.key);
            if (cmp < 0)
                p = p.left;
            else if (cmp > 0)
                p = p.right;
            else
                return p;
        }
        return null;
    }
    
    /**
     * 使用比较器的getEntry版本。 从getEntry分离以获得性能。 (对于大多数方法来说，这是不值得做的，这些方法较少依赖于比较器性能，但在这里是值得的。)
     */
    final Entry<K,V> getEntryUsingComparator(Object key) {
        @SuppressWarnings("unchecked")
            K k = (K) key;
        Comparator<? super K> cpr = comparator;
        if (cpr != null) {
            Entry<K,V> p = root;
            while (p != null) {
                int cmp = cpr.compare(k, p.key);
                if (cmp < 0)
                    p = p.left;
                else if (cmp > 0)
                    p = p.right;
                else
                    return p;
            }
        }
        return null;
    }